경사 하강법(Gradient Descent)

경사 하강법(Gradient Descent)

 

경사 하강법(Gradient Descent)은 머신러닝 및 딥러닝 알고리즘을 학습시킬때 사용하는 방법 중 하나이며 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 극값(최적값)에 이를 때까지 반복하는 것이다.

 

 

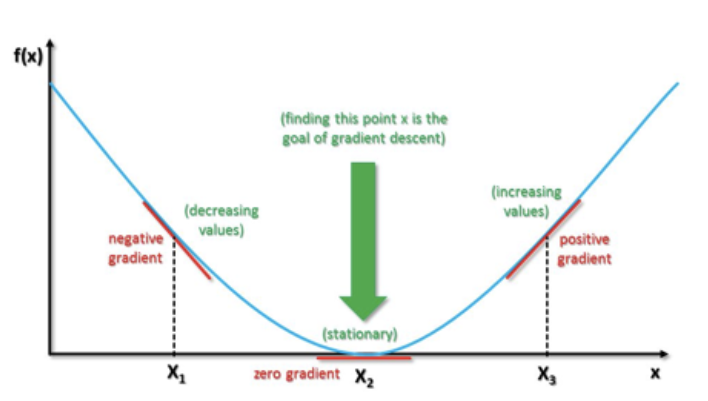
해당 함수의 최소값 위치를 찾기 위해 비용 함수(Cost Function)의 경사 반대 방향으로 정의한 Step Size를 가지고 조금씩 움직여 가면서 최적의 파라미터를 찾으려는 방법이다. 여기에서 경사는 파라미터에 대해 편미분한 벡터를 의미하며 이 파라미터를 반복적으로 조금씩 움직이는 것이 관건이다.

 

 

경사 하강법에서는 학습시 스텝의 크기 (step  size)가 중요하다. 학습률이 너무 작을 경우 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습 시간이 오래걸린다. 그리고 지역 최소값(local minimum)에 수렴할 수 있다. 반대로 학습률이 너무 클 경우 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최소값에서 멀어질 수 있다.

 

경사 하강법에도 약점이 있다. 경사 하강법은 현재 위치에서의 기울기를 사용하기 때문에 지역 최소값에 빠질 수 있다. 또한 무작위 초기화(random initialization)로 인해 알고리즘이 전역 최소값이 아닌 지역 최소값에 수렴할 수 있다. 또한 평탄한 지역을 지나기 위해서 시간이 오래 걸리고 일찍 멈추어서 전역 최소값에 도달하지 못할수도 있다.

 

이와 같은 문제점을 해결하기 위해 사용하는 방법이 모멘텀이다. 쉽게 말해 기울기에 관성을 부과하여 작은 기울기는 쉽에 넘어갈 수 있도록 만든것이다. 즉, 공을 예로 들면 언덕에서 공을 굴렸을때, 낮은 언덕은 공의 관성을 이용하여 쉽게 넘어갈 수 있게 하여 지역 최소값을 탈출 할 수 있게 한다는 뜻이다.

 

모멘텀을 사용하지 않으면 아주 작은 언덕에도 빠져나오지 못할 수 있으며 기울기가 매우 작은 구간을 빠져나오는데에는 아주 오랜 시간이 걸린다.

 

경사 하강법은 전체 데이터를 모두 사용해서 기울기를 계산(Batch Gradient Descent)하기 때문에 학습하는데 많은 시간이 필요하다. 만약 10만개의 데이터가 있을때, 데이터에 업데이트가 있을 때 마다 10만번의 계산을 해야한다. 그래서 학습 데이터가 큰 경우 부담이 있다. 이러한 느린점을 보완하기 위해서 확률적 경사 하강법(Stochastic Gradient Descent)을 사용한다. 이 방법은 매 step에서 딱 한개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 기울기를 계산한다. 확률적 경사 하강법은 아래와 같은 특징이 있다.

·       매우 적은 데이터를 처리하기 때문에 학습 속도가 빠름

·       하나의 샘플만 메모리에 있으면 되기 대문에 큰 데이터셋도 학습이 가능

·       Cost function이 매우 불규칙할 경우 알고리즘이 local minimum을 건너뛰도록 도와주어 global minimum을 찾을 가능성이 높음

·       샘플이 선택이 확률적(Stochastic)이기 때문에 배치 경사 하강법에 비해 불안정

·       Cost function이 local minimum에 이를때 까지 부드럽게 감소하지 않고 위아래로 요동치며 평균적으로 감소

 

 

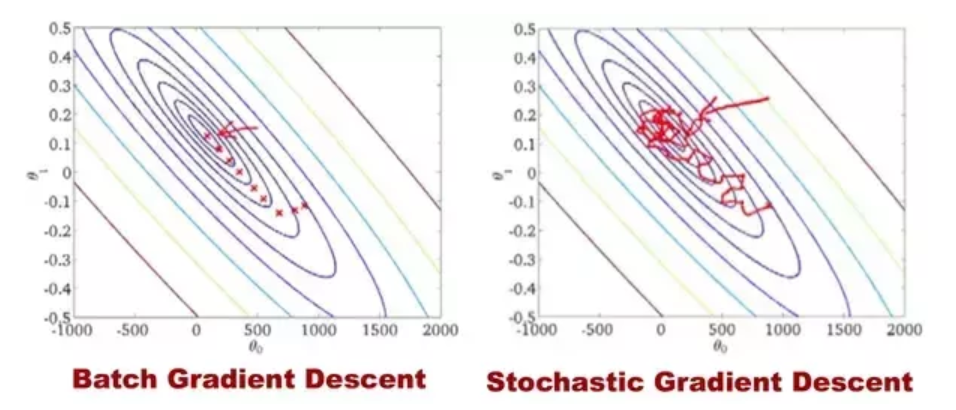
이외에도 Mini-batch Gradient Descent  방식이 있다. 이 방식은 임의의 작은 샘플세트에 대해 gradient를 계산하여 SGD(Stochastic Gradient Descent)에 비해 matrix 연산에 최적화되어 있으며 파라미터 공간에서 덜 불규칙하게 학습한다. 하지만 local minimum에 빠지면 빠져나오기 힘든 단점이 있다.

 

 

[참고자료]

·       https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95

·       https://m.blog.naver.com/PostView.nhn?blogId=2011topcit&logNo=220563609607&proxyReferer=https%3A%2F%2Fwww.google.com%2F

·       https://jaehyeongan.github.io/2019/04/23/%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95-Gradient-Descent/

·       https://bskyvision.com/411

 

 

 

2020-03-15/ Sungwook Kang / http://sungwookkang.com

 

 

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, 경사 하강법, Gradient Descent, 경사 감소법