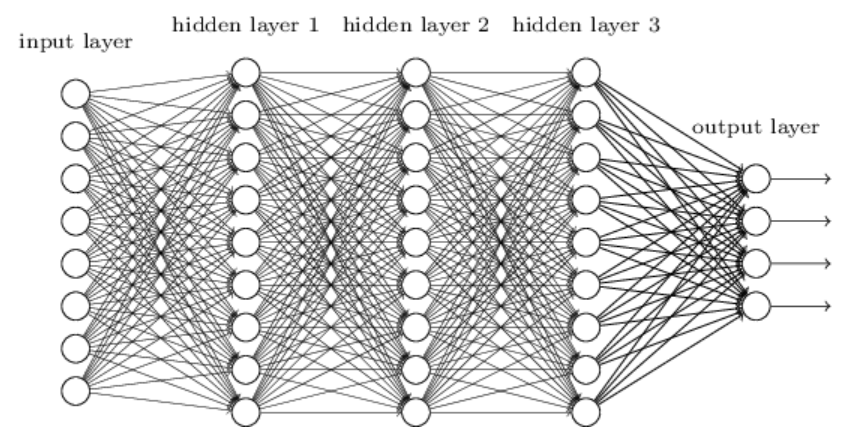
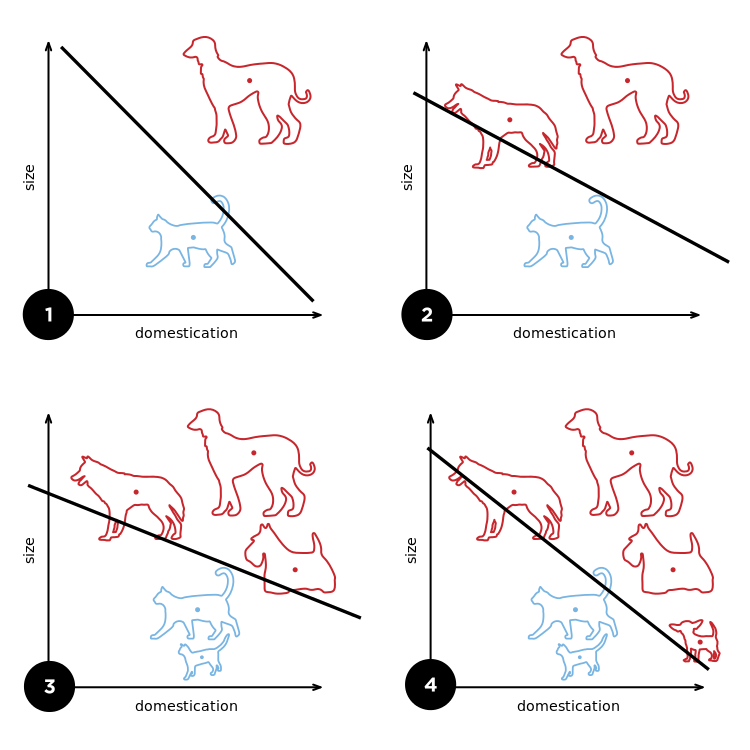
다층 퍼셉트론 (Multi-layer Perceptron) 퍼셉트론은 사람 뇌의 단일 뉴런이 작동하는 방법을 흉내내기 위해 환원 접근법 (reductionist approach)을 이용한다. 이 방법은 초기 가중치를 임의의 값으로 정의하고 예측값의 활성 함수 리턴값과 실제 결과값의 활성 함수 리턴값이 동일하게 나올 때까지 가중치의 값을 계속 수정하는 방법이다. 단층 퍼셉트론의 경우 AND, NAND, OR 논리회로를 계산할 수 있지만 XOR 게이트 연산을 할 수 없다. XOR 게이트는 베타적 논리합 이라 불리는 회로이다. 이 뜻은 한쪽이 1일 때만 1을 출력한다 퍼셉트론 이론은 선형 분류이다. 즉 직선을 이용한 분류는 가능하지만 XOR 게이트와 같은 경우 곡선으로 나눌 수 있기 때문에 비선형 분류이다. ..