Data Science Lab

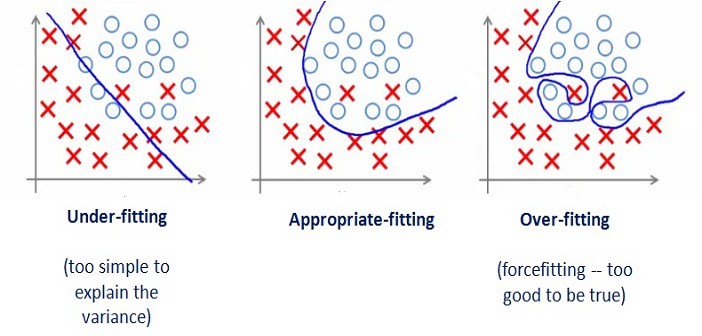
과대적합(Over fitting)과 과소적합(Under fitting)

머신러닝에서 학습과정은 패턴을 발견하기 위해 모델링을 만드는 단계라고 할 수 있다. 일반적으로 모델을 만들 때에는 데이터를, 트레이닝 데이터 (training)와 테스트 데이터(test)를 나누어 사용한다.  트레이닝 데이터를 반복적으로 학습함으로써 테스트 데이터 또는 실제 데이터와 가장 유사한 결과를 만들어 내는 것을 목표로 하고 있다.

하지만 트레이닝 데이터와 테스트 데이터가 비슷하다면 모델의 정확도는 매우 높게 나올 것이다. 하지만 모델이 복잡하다면 트레이닝 데이터와 테스트 데이터의 결과는 다르게 나타날 확률이 높다. 일반적으로 트레이닝 데이터는 실제 데이터를 샘플링 하거나 특정 패턴을 인식시키기 위한 데이터로 트레이닝 데이터에 최적화 되어있으면 실제 데이터에서 오차가 발생할 확률이 크다. 그래서 트레이닝 데이터에 대해서는 높은 정확도를 나타내지만 새로운 데이터에 대해서 예측을 잘 하지 못하는 것을 과대적합(Overfitting )이라고 하며, 반대로 트레이닝 데이터 조차도 정확한 결과를 도출하지 못하면 과소적합(Underfitting)이라고 한다. 과대적합과 과소적합 사이에서 최적화된 절충점을 찾아 모델을 만드는 것이 매우 중요하며 트레이닝 데이터에서 생성된 모델이 일반 데이터에 대해 정확하게 예측되는 모델을  “일반화(Generalization) 되었다” 라고 한다.

아래 그림은 과소적합(Under fitting)과 과대적합(Over fitting)의 이해를 돕기 위해 그림으로 나타낸 것이다.  과소적합의 경우 데이터를 충분히 반영하지 못해(샘플 개수가 충분하지 않는 경우)  잡음이 많이 섞여 있으며, 과대적합의 경우 불필요한 잡음(noise)를 과도하게 모델링에 반영한 상태이다. 우리는 어느정도 오류(noise)를 허용할지 결정하면서 최적의 모델 값을 도출해야 한다.

과대적합이나 과소적합의 문제를 최소화하고 정확도를 높이는 가장 좋은 방법은 더 많고 다양한 데이터를 확보하고, 그 데이터에서 다양한 특징(feature)들을 찾아서 학습에 사용하는 것이다. 즉, 트레이닝 데이터에 따라, 생성된 모델의 정확도가 결정되므로 트레이닝 데이터 세트를 잘 만드는 것이 중요하다.

[참고자료]

https://brunch.co.kr/@gimmesilver/44

https://ko.d2l.ai/chapter_deep-learning-basics/underfit-overfit.html

2020-03-18/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, 과대적합, 과소적합, Over fitting, Under fitting

경사 하강법(Gradient Descent)

경사 하강법(Gradient Descent)은 머신러닝 및 딥러닝 알고리즘을 학습시킬때 사용하는 방법 중 하나이며 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 극값(최적값)에 이를 때까지 반복하는 것이다.

해당 함수의 최소값 위치를 찾기 위해 비용 함수(Cost Function)의 경사 반대 방향으로 정의한 Step Size를 가지고 조금씩 움직여 가면서 최적의 파라미터를 찾으려는 방법이다. 여기에서 경사는 파라미터에 대해 편미분한 벡터를 의미하며 이 파라미터를 반복적으로 조금씩 움직이는 것이 관건이다.

경사 하강법에서는 학습시 스텝의 크기 (step  size)가 중요하다. 학습률이 너무 작을 경우 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습 시간이 오래걸린다. 그리고 지역 최소값(local minimum)에 수렴할 수 있다. 반대로 학습률이 너무 클 경우 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최소값에서 멀어질 수 있다.

경사 하강법에도 약점이 있다. 경사 하강법은 현재 위치에서의 기울기를 사용하기 때문에 지역 최소값에 빠질 수 있다. 또한 무작위 초기화(random initialization)로 인해 알고리즘이 전역 최소값이 아닌 지역 최소값에 수렴할 수 있다. 또한 평탄한 지역을 지나기 위해서 시간이 오래 걸리고 일찍 멈추어서 전역 최소값에 도달하지 못할수도 있다.

이와 같은 문제점을 해결하기 위해 사용하는 방법이 모멘텀이다. 쉽게 말해 기울기에 관성을 부과하여 작은 기울기는 쉽에 넘어갈 수 있도록 만든것이다. 즉, 공을 예로 들면 언덕에서 공을 굴렸을때, 낮은 언덕은 공의 관성을 이용하여 쉽게 넘어갈 수 있게 하여 지역 최소값을 탈출 할 수 있게 한다는 뜻이다.

모멘텀을 사용하지 않으면 아주 작은 언덕에도 빠져나오지 못할 수 있으며 기울기가 매우 작은 구간을 빠져나오는데에는 아주 오랜 시간이 걸린다.

경사 하강법은 전체 데이터를 모두 사용해서 기울기를 계산(Batch Gradient Descent)하기 때문에 학습하는데 많은 시간이 필요하다. 만약 10만개의 데이터가 있을때, 데이터에 업데이트가 있을 때 마다 10만번의 계산을 해야한다. 그래서 학습 데이터가 큰 경우 부담이 있다. 이러한 느린점을 보완하기 위해서 확률적 경사 하강법(Stochastic Gradient Descent)을 사용한다. 이 방법은 매 step에서 딱 한개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 기울기를 계산한다. 확률적 경사 하강법은 아래와 같은 특징이 있다.

·       매우 적은 데이터를 처리하기 때문에 학습 속도가 빠름

·       하나의 샘플만 메모리에 있으면 되기 대문에 큰 데이터셋도 학습이 가능

·       Cost function이 매우 불규칙할 경우 알고리즘이 local minimum을 건너뛰도록 도와주어 global minimum을 찾을 가능성이 높음

·       샘플이 선택이 확률적(Stochastic)이기 때문에 배치 경사 하강법에 비해 불안정

·       Cost function이 local minimum에 이를때 까지 부드럽게 감소하지 않고 위아래로 요동치며 평균적으로 감소

이외에도 Mini-batch Gradient Descent  방식이 있다. 이 방식은 임의의 작은 샘플세트에 대해 gradient를 계산하여 SGD(Stochastic Gradient Descent)에 비해 matrix 연산에 최적화되어 있으며 파라미터 공간에서 덜 불규칙하게 학습한다. 하지만 local minimum에 빠지면 빠져나오기 힘든 단점이 있다.

[참고자료]

·       https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95

·       https://m.blog.naver.com/PostView.nhn?blogId=2011topcit&logNo=220563609607&proxyReferer=https%3A%2F%2Fwww.google.com%2F

·       https://jaehyeongan.github.io/2019/04/23/%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95-Gradient-Descent/

·       https://bskyvision.com/411

2020-03-15/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, 경사 하강법, Gradient Descent, 경사 감소법

순전파(Feedforward)와 역전파(Backpropagation) 개념

다층 퍼셉트론(Multi-layer Perceptron, MLP)으로 학습 한다는 것은 최종 출력값과 실제값의 오차가 최소화 되도록 가중치와 바이어스를 계산하여 결정하는 것이다. 순전파 (Feedforward) 알고리즘 에서 발생한 오차를 줄이기 위해 새로운 가중치를 업데이트하고, 새로운 가중치로 다시 학습하는 과정을 역전파 (Backpropagation) 알고리즘 이라고 한다. 이러한 역전파 학습을 오차가0에 가까워 질 때까지 반복한다. 역전파 알고리즘을 실행할때 가중치를 결정하는 방법에서는 경사하강법이 사용된다.

[순전파 (Feedfoward)]

입력층에서 은닉층 방향으로 이동하면서 각 입력에 해당하는 가중치가 곱해지고, 결과적으로 가중치 합으로 계산되어 은닉층 뉴런의 함수 값(일반적으로 시그모이드(Sigmoid) 사용)이 입력된다. 그리고 최종 결과가 출력된다.

[역전파 (Backpropagation)]

역전파 알고리즘은 input과 output 값을 알고 있는 상태에서 신경망을 학습 시키는 방법이다. 이 방법을 Supervised learning(지도학습)이라고 한다. 초기 가중치, weight 값은 랜덤으로 주어지고 각각 노드들은 하나의 퍼셉트론으로, 노드를 지날때 마다 활성함수를 적용한다.

역전파 알고리즘의 수식은 아래와 같다.

·       target : 출력의 기대 값

·       output : 실제 출력 값

·       E : 오차

역전파 알고리즘도 한계점은 있다. 은닉층에서 시그모이드(Sigmoid) 함수를 사용하면 가중치 조정을 위해 경사감소법을 사용하는데, 계단형식 함수를 미분가능하도록 곡선화 한다. 은닉층이 깊어질 수록 가중치가 0으로 수렴하며 정확성이 감소한다. 이러한 역전파 알고리즘의 문제점을 해결하기 위해 ReLu 알고리즘을 사용한다. ReLu는 x 값이 0이하이면 0을 출력, 0 이상이면 비례함수를 적용하여 max(0,x) 함수를 사용한다.

[참고자료]

·       https://wikidocs.net/37406

·       https://ko.wikipedia.org/wiki/%EC%97%AD%EC%A0%84%ED%8C%8C

·       https://sacko.tistory.com/19

·       https://m.blog.naver.com/samsjang/221033626685

·       https://goofcode.github.io/back-propagation

·       https://gomguard.tistory.com/182

2020-03-14/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning,다층 퍼셉트론, Multi-layer perceptron, 역전파, 순전파 , Backpropagation, Feedforward

다층 퍼셉트론 (Multi-layer Perceptron)

퍼셉트론은 사람 뇌의 단일 뉴런이 작동하는 방법을 흉내내기 위해 환원 접근법 (reductionist approach)을 이용한다. 이 방법은 초기 가중치를 임의의 값으로 정의하고 예측값의 활성 함수 리턴값과 실제 결과값의 활성 함수 리턴값이 동일하게 나올 때까지 가중치의 값을 계속 수정하는 방법이다.

단층 퍼셉트론의 경우 AND, NAND, OR 논리회로를 계산할 수 있지만 XOR 게이트 연산을 할 수 없다. XOR 게이트는 베타적 논리합 이라 불리는 회로이다. 이 뜻은 한쪽이 1일 때만 1을 출력한다

퍼셉트론 이론은 선형 분류이다. 즉 직선을 이용한 분류는 가능하지만 XOR 게이트와 같은 경우 곡선으로 나눌 수 있기 때문에 비선형 분류이다.

이러한 제약사항을 보완하기 위해 나온것이 다층 퍼셉트론 (Multi-layer Perceptron, MLP)이다. 단층 퍼셉트론과 다층 퍼셉트론의 차이점은 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가하였다. 이렇게 입력과 출력 사이에 추가된 층을 은닉층(hidden layer)이라 한다. XOR 게이트는 기존의 AND, NAND, OR 게이트를 조합하여 만들 수 있기 때문에 퍼셉트론에서 층을 계속 추가하면서 만들 수 있다. 이렇게 층을 여러겹으로 쌓아가면 선형 분류만으로 풀지 못했던 문제를 비선형적으로 풀 수 있게 된다.

다층 퍼셉트론은 은닉층이 1개 이상인 퍼셉트론을 의미한다. 은닉층이 2개일수도 있고 수십, 수백개 일수도 있다. 아래 그림과 같이 은닉층이 2개 이상인 신경망을 심층 신경망 (Deep Neural Network, DNN)이라고 한다.  학습을 시키는 신경망이 심층 신경망일경우 심층 신경망을 학습시칸다고 하여 딥러밍(Deep Learning)이라고 한다.

[참고자료]

·       https://en.wikipedia.org/wiki/Multilayer_perceptron

·       https://wikidocs.net/24958

2020-03-12/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning,신경망, 뉴럴 네트워크,퍼셉트론, Perceptron, 다층 퍼셉트론, Multi-layer perceptron

단층 퍼셉트론 (Single-layer Perceptron)

퍼셉트론 (Perceptron)은 1957년 코넬 항공 연구소에 근무하던 프랑크 로젠블라트(Frank Rosenblatt)가 MCP 뉴런 모델을 기초로 퍼셉트론이라는 알고리즘을 고안하였다. 퍼셉트론은 하나의 MCP 뉴런이 출력신호를 발생할지 안할지 결정하기 위해 MCP 뉴런으로 들어오는 각 입력값에 곱해지는 가중치 값을 자동적으로 학습하도록 한 모델이며 입력 벡터를 두 부류(class)로 구분하는 선형 분류기 이다. 퍼셉트론은 신경망(딥러닝)의 기원이 된 알고리즘이다.

퍼셉트론은 다수의 신호를 입력 받아 하나의 신호를 출력한다. 여기서 말하는 신호는 전류처럼 흐름이 있는것을 뜻하며, 흐름의 상태 정보를 앞으로 전달한다. 아래 그림은 x1, x2라는 입력 신호에 w1, w2라는 가중치를 부여하여 y라는 신호를 출력한다.

입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다. 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력하게 된다. 이를 “뉴런이 활성화 한다” 라고 표현 할 수 있다. 그 한계를  “임계값” 이라고 한다. 임계값은 보통 θ(세타)로 표현된다. 퍼셉트론은 복수의 입력 신호 각각에 고유한 가중치를 부여하게 된다. 가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용된다. 즉, 가중치가 클수록 해당 신호가 그만큼 더 중요하다는 뜻이다.

위 그림에서 x는 입력 벡터 값을 나타내며, w는 가중치를 나타낸다. 바이어스 입력값은 x0, 바이어스 기울기는  w0로 표기했으며 f는 활성홤수를 나타낸다.

·       임계치(threshold): 어떠한 값이 활성화되기 위한 최소값

·       가중치(weight): 선형 경계의 방향성 또는 형태를 나타내는 값

·       바이어스(bias): 선형 경계의 절편을 나타내는 값으로써, 직선의 경우는 y절편으로 표시

·       net값: 입력값과 가중치의 곱을 모두 합한 값

·       활성홤수(activation function): 뉴런에서 계산된 net값이 임계치보다 크면 1을 출력하고, 임계치보다 작은 경우에는 0을 출력하는 함수

·       뉴런(neuron): 인공신경망을 구성하는 가장 작은 요소로써, net값에 따라 활성(1) 비활성(0)을 출력

아래 그림은 더 많은 훈련 데이터가 추가됨에 따라 선형 경계를 업데이트하는 퍼셉트론을 보여주는 다이어그램이다.

퍼셉트론으로는 AND, NAND, OR 게이트의 논리회로를 표현할 수 있다.

[AND 게이트]

AND 게이트는 입력이 둘이고 출력이 하나인 대표적인 퍼셉트론 예시이다.  입력값이 모두 1일때 1을 출력한다.

예를들어 (w1, w2, θ)의 값을 (0.5, 0.5, 0.8)이라고 가정하였을때 계산이다.

·       (0*0.5) + (0*0.5) = 0.0         <  0.8        -> 0

·       (0*0.5) + (1*0.5) = 0.5        <  0.8        -> 0

·       (0*0.5) + (0*0.5) = 0.5        <  0.8        -> 0

·       (1*0.5) + (1*0.5) = 1.0         >  0.8        -> 1

[NAND 게이트]

AND게이트에 NOT 연산을 한것으로, AND 게이트 결과값의 반대이다.

[OR 게이트]

입력 신호중 하나 이상이 1이면 1이 출력된다.

[단층 퍼셉트론의 한계]

단층 퍼셉트론은 AND, NAND, OR 논리회로를 계산할 수 있지만 XOR 게이트 연산을 할 수 없다. XOR 게이트는 베타적 논리합 이라 불리는 회로이다. 이 뜻은 한쪽이 1일 때만 1을 출력한다.

퍼셉트론 이론은 선형 분류이다. 즉 직선을 이용한 분류는 가능하지만 XOR 게이트와 같은 경우 곡선으로 나눌 수 있기 때문에 비선형 분류이다. 이러한 제약사항을 보완하기 위해 나온것이 다중 (Multi-layer Perceptron)이다.

[참고자료]

·       https://en.wikipedia.org/wiki/Perceptron

·       https://untitledtblog.tistory.com/27

·       https://eehoeskrap.tistory.com/137

·       https://excelsior-cjh.tistory.com/169

2020-03-11/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, AI, 신경망, 뉴럴 네트워크, 강화학습, 지도학습, 자율학습, Supervised Learning, Unsupervised Learning, Reinforcement Learning, 퍼셉트론, Perceptron, 단층 퍼셉트론, Single-layer perceptron

머신러닝 학습 방법(Supervised, Unsupervised, Reinforcement)

머신러닝의 데이터 학습 방법에는 지도 학습 (Supervised Learning)과 자율 학습 (Unsupervised Leaning), 강화 학습(Reinforcement Learning) 3가지 타입이 있다.

지도 학습 (Supervised Learning)과 자율 학습 (Unsupervised Leaning)에 사용되는 알고리즘은 아래 그림과 같이 나눌 수 있다.

[지도 학습 (Supervised Learning)]

지도 학습(Supervised Learning)은 데이터에 대한 레이블(Label)-명시적인 정답-이 주어진 상태에서 컴퓨터를 학습시키는 방법이다. 이렇게 구성된 트레이닝 데이터셋으로 학습이 끝나면, 레이블(label)이 지정되지 않은 테스트 데이터셋(test set)을 이용해서, 학습된 알고리즘이 얼마나 정확히 예측(Prediction)하는지를 측정할 수 있다.

이러한 평가를 위해 교차검증(Cross-Validation)이 이용되며 이를 위해 훈련 집합(A Training Set), 검증 집합(A Validation Set), 테스트 집합(A Test Set)으로 나눈다. 교차 검증을 통하여 훈련된 각 함수에 대해 정밀도(Precision)와 재현율(Recall)를 측정 할 수 있다.

훈련 데이터는 일반적으로 입력 개체에 대한 속성을 벡터 형태로 포함하고 있으며 각각의 벡터에 대해 원하는 결과가 무엇인지 표시되어 있다. 이렇게 유추된 함수 중 연속적인 값을 출력하는 것을 회귀분석(Regression)이라 하고 주어진 입력 벡터가 어떤 종류의 값인지 표식 하는것을 분류(Classification)라 한다. 지도학습기(Supervised Learner)가 하는 작업은 훈련 데이터로부터 주어진 데이터에 대해 예측하고자 하는 값을 올바로 추측해내는 것이다. 이 목표를 달성하기 위해서는 학습기가 "알맞은" 방법을 통하여 기존의 훈련 데이터로부터 나타나지 않던 상황까지도 일반화하여 처리할 수 있어야 한다. 훈련데이터로부터 하나의 함수가 유추되고 나면 해당 함수에 대한 평가를 통해 파라미터 최적화를 한다. 지도 학습은 직관적이기 때문에 다른 학습법에 비해 상대적으로 이해하기가 쉽지만, 정확한 학습 결과를 얻으려면 고품질의 많은 학습 데이터셋이 필요하다.

[자율 학습 (Unsupervised Leaning)]

자율 학습(Unsupervised Learning)은 기계학습의 일종으로 데이터가 어떻게 구성되었는지를 알아내는 문제의 범주에 속한다. 이 방법은 지도 학습(Supervised Learning) 혹은 강화 학습(Reinforcement Learning)과 달리 입력 값에 대한 목표치가 주어지지 않는다. 자율학습은 통계의 밀도 추정(Density Estimation)과 깊은 연관이 있다. 이러한 자율학습은 데이터의 주요 특징을 요악하고 설명할 수 있다. 자율학습의 예로는 클러스터링(Clustering), 독립 성분 분석(Independent Component Analysis), 연관성 규칙, 데이터 축소 등이 있다.

자율 학습은 학습할 데이터셋만 있으면 스스로 학습하기 때문에 편리하기는 하지만 지도 학습에 비해 어려우며, 특정 결과에 대한 가이드가 없기 때문에 기대했던 것과 다른 결과가 나올 수도 있다.

[강화 학습 (Reinforcement Learning)]

강화 학습(Reinforcement learning)은 기계 학습의 한 영역이다. 행동심리학에서 영감을 받았으며, 어떤 환경 안에서 정의된 에이전트가 현재의 상태를 인식하여, 선택 가능한 행동들 중 보상을 최대화하는 행동 혹은 행동 순서를 선택하는 방법이다. 즉 훈련을 잘 따르면 보상(reward)를 주고 못하면 벌(punishment)을 주어 감독관이 원하는 방향으로 학습을 하게 된다.

지도 학습처럼 입력과 출력이 명확한 관계를 갖고 있는 상황이 아니라 환경과의 상호 작용의 결과로서 학습을 하거나 경우의 수가 너무 많아 옳고 그름에 대해 사전에 명확하게 기술하기 어려운 환경에 적합한 학습방법이다.

이러한 문제는 매우 포괄적이기 때문에 게임 이론, 제어이론, 운용 과학, 정보 이론, 시뮬레이션 기반 최적화, 다중 에이전트 시스템, 군집 지능, 통계학, 유전 알고리즘 등의 분야에 사용된다.

[참고자료]

l  https://bigdata-madesimple.com/machine-learning-explained-understanding-supervised-unsupervised-and-reinforcement-learning/

l  https://ko.wikipedia.org/wiki/%EA%B0%95%ED%99%94_%ED%95%99%EC%8A%B5

2020-03-08/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, AI, 신경망, 뉴럴 네트워크, 강화학습, 지도학습, 자율학습, Supervised Learning, Unsupervised Leaning, Reinforcement Learning

인공지능 /  머신러닝 / 딥러닝 개념

인공지능 (Artificial Intelligence)과 머신러닝 (Machine Learning), 딥러닝 (Deep Learning) 개념에 대해서 살펴본다.

[인공지능 (Artificial Intelligence)]

인간의 지능으로 할 수 있는 사고, 학습, 자기 개발 등 컴퓨터가 대체할 수 있도록 하는 방법을 연구하는 분야이다.

[머신러닝 (Machine Learning)]

사람이 학습하듯 컴퓨터에게 사람이 데이터를 입력시켜 학습을 시키는 방식으로, AI는 정확한 결과를 예측 할 수 있도록 제공된 학습 데이터를 다양한 알고리즘을 통하여 스스로 학습한다. 머신러닝은 정해진 명령보다 데이터를 기반으로 예측이나 결정을 이끌어 내기 위해 특정한 모델을 구축하는 방식으로 모델을 구축함으로써 입력하지 않은 정보에 대해서다 판단이나 결정을 할 수 있게 된다.

머신러닝은 현재 많은 분야에서 활용되고 있으며 문자 인식, 안면 인식, 자동 번역, 챗봇 등의 자연어 처리 분야와, 음성 인식, 필기 인식, 텍스트 마이닝, 스팸 필터, 추천 시스템 등의 정보 검색 엔진, 유전자 분석, 단백질 분류 등 다양한 곳에서 사용되고 있다.

[딥러닝 (Deep Learning)]

 머신러닝에서 발전된 형태로 사람이 학습할 데이터를 입력하지 않아도 스스로 학습하고 예측한다. 이러한 모델은 인간의 신경망을 본딴 인공 신경망에서 발전한 것이다. 딥러닝은 머신러닝 기법인 Feature Learning (또는 Representation Learning) 중 하나 이다. 딥러닝은 인공신경망에서 발전한 심층신경망 (Deep Neural Network, DNN)인데, 여러 신경들이 다음 신경에 신호를 전달하는 방식의 모델이기에 딥러닝을 계층적 Feature Learning (또는 Representation Learning)라고 부른다.

딥러닝의 가장 대표적인 예가 2016년 이세돌 9단과 바둑 대결을 펼쳤던 구글의 “알파고”이다. 당시 알파고는 바둑 기보를 보고 스스로 바둑 전략을 학습했다.

페이스북은 딥러닝 기술을 적용해 2014년 “딥페이스”라는 얼굴 인식 알고리즘을 개발했다.

이외에도 MS, IBM 등 많은 테크기업들이 딥러닝을 적용한 제품을 만들었다.

위에 정의된 내용으로 동물을 판단하는 방법을 살펴보자. 머신러닝의 경우 개의 특징을 추출하는 것은 사람이 하며, 추출된 특징을 학습하여 고양이인지, 개인지 판단하는 것은 기계가 한다. 반면 딥러닝은 특징을 추출하고 학습하는 모든 과정을 기계가 한다.

2020-03-07/ Sungwook Kang / http://sungwookkang.com

인공지능,  Artificial Intelligence, 머신러닝, Machine Learning, 딥러닝, Deep Learning, AI, 신경망, 뉴럴 네트워크, 구글 알파고, 페이스북 딥페이스